三角函数的定义

    三角形边与角之间量的关系，是由几种随着角的改变而变化的辅助量來建立的，这些辅助量我們叫它三角函數。借助三角函数我们可以用来解三角形。但是三角函數的用处，不仅限于用來解三角形，在許多其它数学科目中，以及在物理学、工程学等也要应用它們。因而研究三角函数非常重要。
    任何研究，先要有个起点。研究三角函数的起点就是它的名称和表示法，这就是三角函数的定义。任一角的三角函数有以下六种：正弦、余弦、正切、余切、正割、余割。
    它們用以下六种符号來表示： sin 、 cos 、 tg 、 ctg 、 sec 、 csc 。在上列函数符号后，必須附以对应于函数値的变数値（角）。例如一角α 的正弦，用符号來表示则为：sinα。
    光有符号是不够的，关键是这些符号的定义。其实三角函数来自于对三角形研究的需要，其定义也来自三角形。现以锐角三角形为研究切入点：

    如图，取任意一锐角 α ，以此角的顶点为圆心，任一长为半径作一圆，使得这个角成为圆心角。设以 R 代表半径之长。为了区别构成此角的两个半径OA和OB，设角 α 变化时，半径 OA 的位置不变，仅半径 OB 随之转动。我們將固定的半径 OA 叫做角的始边，將转动的半径 OB 叫做角的终边。这样，在这个以 α 为圆心角的圆上能画出一些特殊线段，三角函数就被定义为这些特殊线段与半径之比。为了作出这些特殊线段，除弧 AB 外，我們还需利用弧 AB 的延长弧，及与 OA 直交的半径 OM 。
    下面是由通过锐角 α 得出的三角函数的定义：

1）由终边的端点向始边所引的垂线（ BC ）叫做正弦线，正弦线 BC 与半径之比叫做已知
角的正弦（sin α =	BC	）
	R

2）由圆心向正弦线所引的垂线（ OC ）叫做余弦线，余弦线与半径之比叫做已知角的余弦
（cos α =	OC	）
	R

3）由始边的端点向上所引的圆切线与终边的延长线相交的线段( AD ）叫做正切线，正切
线与半径之比叫做已知角的正切（tg α =	AD	）
	R

4）由垂直于始边的半径（OM）端点所引的圆切线与终边的延长线相交的线段（ ME ）叫做
余切线。余切线与半径之比叫做已知角的余切(ctg α =	ME	）
	R

5）从圆心到正切线終点的线段（ OD ）叫做正割线，正割线与半径之比叫做已知角的正割
（sec α =	OD	）
	R

6）从圆心到余切线（ME）终点的线段（ OE ）叫做余割线，余割线与半径之比，叫做已知
角的余割（csc α =	OE	）
	R

    我们通过锐角定义三角函数时涉及到辅助圆，那三角函数的值与这圆的大小有关吗？见下图：

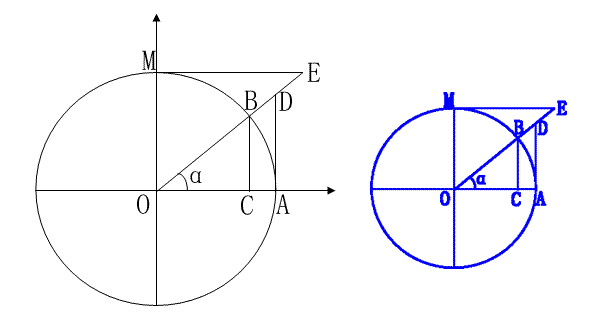
    左右两图为同一大小的角所作的半径不同的辅助圆。将两图合并如下：

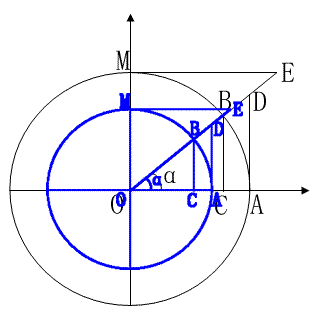
    可见，虽然辅助圆半径不同，但为计算角度值相同的角的三角函数值所建立的三角形是相似三角形，所以，三角函数的值仅决定于角的大小，与辅助圆无关。实际上辅助圆只是为了帮助我们思考而已。
    刚刚我们通过锐角定义了三角函数，也就是说这角的范围在0度到90度，显然这时的三角函数都为正值。但在实际中，角可能大于90度，这时的三角函数情况如何？也就是我们要在锐角的基础上对三角函数的内涵进行扩展。
    我们知道，通过锐角定义三角函数时借助了直观的图形，当时讨论的范围仅在整圆的四分之一区域内，这种区域称象限，该区域是通过圆心在圆內作水平的和垂直的二直径 NA 与 PM ，将圆分成四部分而建立的。如下图所示：

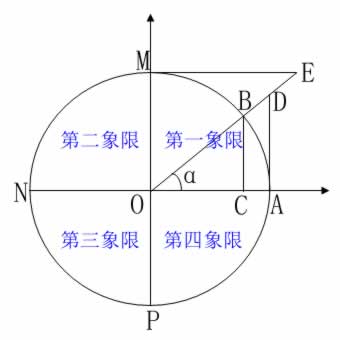
    如：AOM 叫做第一象限，也就是我们通过锐角定义三角函数的区域；MON 叫做第二象限；NOP 叫做第三象限；POA 叫做第四象限。这样，我们在扩展三角函数的内涵时，只需将前面锐角的动边按逆时针方向转到第二、第三、第四象限即可获得扩展后的结果。
    据此，我们可画出动边在第二象限时的辅助图形。
    这是一种科学研究的方法：先定义一个点，然后扩展它的范围，获得更广的内涵。
    对科学来说，研究范围的扩大，意味着构建这个范围的可变量的概念也扩大了，事实也正是如此。
研究锐角时，以锐角的顶点为圆心建立的圆，因研究只局限在第一象限，正弦线、余弦线、正切线、余切线、正割线、余割线，这些线段只要考虑大小，不必考虑方向，所以锐角的三角函数值都为正值。但现在角大于了90度，终边落在其它象限，这就要考虑线段的方向。
    事实上，当角大于90度后，研究需借助以角顶点为圆心，终边为半径的整个圆来进行。这时，圆点变成原点，过原点分割圆为四个象限的相互垂直的线被抽象出来成为平面坐标系的两个轴，这时位于原点两边线段的数值即使大小相同，但因以原点为中心的方向不同，其值也不同。一为正，另一为负。此时，计算三角函数的线段除大小外，还要考虑方向。具体作图如下：

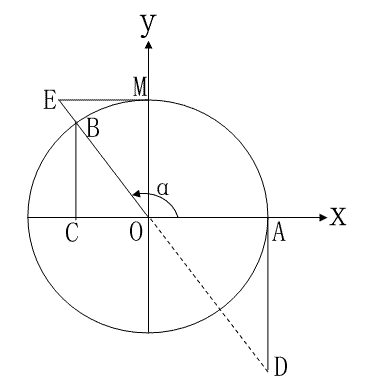
    现在我们根据上图来分析一下，当角大于90度，小于180度时该角三角函数的情况。
    由图可见，辅助线段BC、OE在原点的正方向，所以为正值；而辅助线段OC、AD、ME、OD在原点的反方向，所以为负值。
    同样，当角度值落在第三、第四象限时也可如法分析。
    最终，可得到三角函數的广义表示：三角函数值是由三角函数线与半径之比及三角函数线的方向所决定的正数或负数。
    可用图像直观表示三角函数值在各象限的正、负：

正弦及余割	余弦及正割	正切及余切

    上面，我们按照前辈数学家定义三角函数的步骤，从锐角开始，拓展到360度以内的角，这是这个定义的基础。若要进一步拓展，就要考虑角的转动方向和以原点为圆心，动边旋转多个360度所形成角的情况。
    前者，角的转动方向。我们考虑的是逆时针转动形成的角，若角是顺时针转动形成的，那两种方式形成的角有一个属性是不同的，那就是转动方向。因我们最初定义时是把逆时针转动的角作为正值看待的，所以现在考虑顺时针转动形成的角就要把它作为负值看待，以示区别。
    为将定义拓展，我们就要看看角为负值时与前面角为正值是有何种联系。下面我们借助辅助图来思考。

两角和与两角差：
　

sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ + cosα sinβ 　 tanα  + tanβ tan(α + β) = 　 1 +  tanα tanβ

倍角公式：
　

sin2α = 2sinα cosα cos2α = cos2α - sin2α = 1 - 2sin2α = 2cos2α - 1 　 2tanα tan2α = 　 1 - tan2α

和积互化公式：

α + β 　 α - β sinα + sinβ = 2sin cos 　 2 　 2 　 α + β 　 α - β sinα - sinβ = 2cos sin 　 2 　 2 　 α + β 　 α - β cosα + cosβ = 2cos cos 　 2 　 2 　 α + β 　 α - β cosα - cosβ =-2sin sin 　 2 　 2