|
从菱形两条对角线的交点分别向各边引垂线,求证:连结各垂足的四边形是菱形
提示思路:对于几何“文字题”,从分析题设,结论,画图;写已知,求证,直至完成证明,每一步骤都不可缺。对于这类问题,首先根据题设画出准确图形,根据题设及图形翻译成数学语言,即写出已知与求证,然后再去找思路。
已知:菱形ABCD对角线AC,BD相交于点O,ON⊥AD,OM⊥BC,OE⊥AB,OF⊥DC,点N,M,E,F分别为垂足。
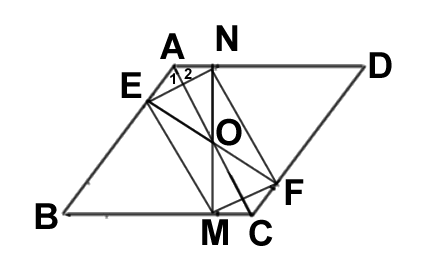
求证:矩形EMFN是矩形。
判定四边形是矩形的常用方法是:
一个角是直角的平行四边形
对角线相等的平行四边形是矩形
有三个角是直角的四边形
由此,本例至少可找到三种证明途径:
思路一:利用“一个角是直角的平行四边形是矩形”打开思路
∵四边形ABCD是菱形
∴AD∥BC
∵OM⊥BC,∴OM⊥AD
又∵ON⊥AD,过O只能作一条直线垂直于AD
∴M、N、O在一条直线上
同理:E、F、O也在同一条直线上
∵菱形ABCD中,∠1=∠2(菱形性质定理2)
又∵OE⊥AB,ON⊥AD
∴OE=ON
同理:OE=OM,OM=OF
∴OE=OF,OM=ON
∴四边形EMFN是平行四边形(平行四边形判定定理3)
∵OE=OM=ON
∴∠OEM=∠OME,∠OMF=∠OFM
∵∠OEM+∠OME+∠OMF+∠OFM=90°×2
∴∠OME+∠OMF=90°,即∠EMF=90°
∴ EMFN是矩形,(一个角是直角的平行四边形是矩形)
思路2:利用“对角线相等的平行四边形是矩形”打开思路
仿思路1可证得四边形EMFN为平行四边形,又∵OE=OM=ON=OF
∴OE+OF=OM+ON,即EF=MN
∴ EMFN为矩形(对角线相等的平行四边形是矩形)
思路3:利用“有三个角是直角的四边形”是矩形打开思路
仿思路1可证得∠EMF=90°
同理可证:∠MFN=90°,∠MEN=90°
∴四边形EMFN为矩形(有三个角是直角的四边形是矩形)
小结:该题把平行四边形、矩形、菱形、正方形串为一体,有一定难度。这就要求我们,从实践中来(学习定义、定理、性质)──上升为理论(理解熟记定义、定理、性质)──指导实践(应用定义、定理、性质去分析解题思路)。在学习中,只要抓住这一学习规律,反复学习,必见成效。尽管平行四边形、矩形、菱形、正方形各种关系盘根错结,采取对比的学习方法,理顺各种从属关系,有意应用学习“规律”,将会收效显著,阅者可在学习中试一试。
|